A lasso regression analysis was conducted to identify a subset of variables from a pool of 6 quantitative predictor variables that best predicted a quantitative response variable measuring the number of people employed. Quantitative predictor variables include Gross National Product (GNP), GNP implicit price deflator (1954=100), number of unemployed, number of people in the armed forces, ‘noninstitutionalized’ population ≥ 14 years of age, and the year (time).
Because of the small size of the data set (N=16), data were not split into training and test sets.
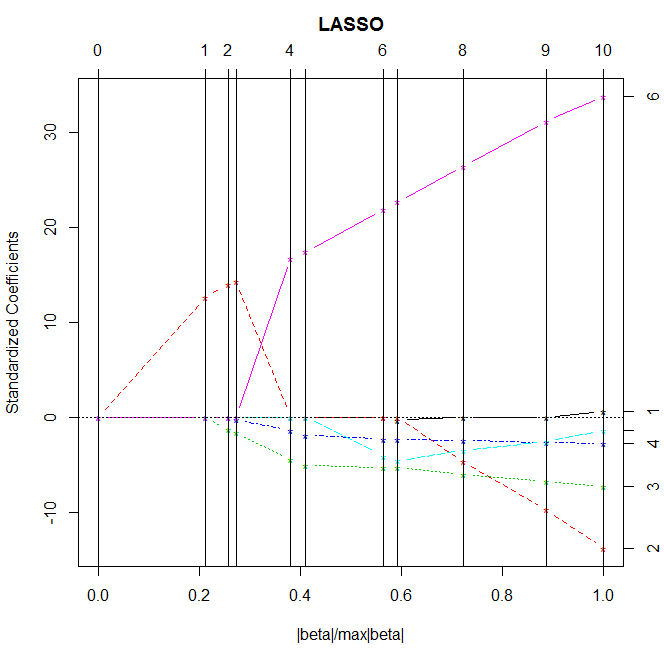
Of the 6 predictor variables, only 2 were retained in the selected model. During the estimation process, year and GNP were most strongly associated with number of people employed. The final model accounted for 97.4% of the variance in the response variable.
Figure 1. Change in the coefficients at each step
Source code in F#:
#load "packages/FsLab/FsLab.fsx" open RDotNet open RProvider open RProvider.lars open RProvider.datasets open RProvider.graphics open Deedle let longley : Frame<int, string> = R.longley.GetValue() let longY = longley?Employed let longX = R.as_matrix(longley.Columns.[ ["GNP.deflator"; "GNP"; "Unemployed"; "Armed.Forces"; "Population"; "Year"] ]) let fit = R.lars(x=longX, y=longY) R.summary fit R.plot fit
Which created the following output:
Call:
lars::lars(x = fsr_9628_42, y = fsr_9628_43)
R-squared: 0.995
Sequence of LASSO moves:
GNP Unemployed Armed.Forces Year GNP Population GNP.deflator GNP GNP.deflator GNP.deflator
Var 2 3 4 6 -2 5 1 2 -1 1
Step 1 2 3 4 5 6 7 8 9 10
LARS/LASSO
Call: lars::lars(x = fsr_9628_42, y = fsr_9628_43)
Df Rss Cp
0 1 185.009 1976.7120
1 2 6.642 59.4712
2 3 3.883 31.7832
3 4 3.468 29.3165
4 5 1.563 10.8183
5 4 1.339 6.4068
6 5 1.024 5.0186
7 6 0.998 6.7388
8 7 0.907 7.7615
9 6 0.847 5.1128
10 7 0.836 7.0000